Statistische Maßzahlen für Lage und zentrale Tendenz
Modalwert/Modus
Median
Berechnung des Medians
In diesem Abschnitt wird die Formel zur Berechnung des Medians erläutert.
Quantile
In diesem Abschnitt wird gezeigt, wie sich das Konstruktionsprinzip des Medians verallgemeinern lässt und wie die Lage einer Verteilung mit Quantilen im Detail beschrieben werden kann.
Arithmetisches Mittel
Berechnung des arithmetischen Mittels
In diesem Abschnitt wird die Formel zur Berechnung des arithmetischen Mittels erläutert.
Mittelwerte im Vergleich
Zusammenfassung
Praktische Umsetzung mit Statistiksoftware
Beispieldaten herunterladen: dat.csv
Datenbeispiel
Unser Beispieldatensatz (hypothetisches Datenbeispiel) liegt als CSV-Datei vor. Die Daten können mit der read.csv-Funktion eingelesen werden (der korrekte Pfad zum Speicherort muss angegeben werden):
dat <- read.csv("C:/... Pfad .../dat.csv")Die Funktion erzeugt ein Objekt vom Typ data.frame, dem wir links vom Zuweisungspfeil (<-) den Namen "dat" geben.
Der Datensatz enthält u.a. die Variablen punkte (erzielte Punktzahl in einem Test), schlafdauer (Schlafdauer in der Nacht vor dem Test in Std.), lernzeit (insgesamt für den Test aufgewendete Lernzeit in Std.) und lsport (Lieblingssportart). Einzelne Variablen können als Datensatzname$Variablenname angesprochen werden, z.B.:
dat$punkte
[1] 93.0 76.5 79.5 85.0 66.5 71.0 56.5 77.0 59.0 63.5 72.0 70.0 96.0 72.0 62.5 76.5 86.0 57.5
[19] 60.0 73.5 64.5 54.0 85.0 64.0 57.5 54.0 76.5 41.0 58.5 87.5 62.5 62.5 100.5 86.0 66.5 79.5
[37] 77.0 67.5 58.5 92.5 94.5 77.0 76.0 67.0 44.5 86.5 70.0 81.5 90.5 78.0 80.5 74.0 56.5 60.0
[55] 83.0 70.0 49.0 57.0 48.0 70.5 96.5 106.0 65.5 86.5 87.5 89.5 64.0 86.0 62.0 94.5 52.0 73.5
[73] 77.0 83.5 62.5 52.5 51.5 86.5 70.5 57.5 68.0 103.0 79.0 75.0 113.5 78.0 104.5 84.5 63.5 46.0
[91] 102.5 77.0 73.5 71.0 106.0 79.0 77.5 87.0 92.5 11.5 83.5 86.5 78.5 67.5 71.0 61.5 31.0 50.5
[109] 87.5 66.5 67.0 60.5 61.5 83.5 66.0 97.0 79.5 83.5 82.0 63.0Die Ausgabe zeigt die 120 beobachteten Werte der Variable punkte.
Für einen ersten Überblick über die Struktur des Datensatzes und die im Datensatz enthaltenen Variablen kann die Funktion str(dat) verwendet werden:
str(dat)liefert das folgende Ergebnis:
'data.frame': 120 obs. of 25 variables:
$ X : int 94 66 78 28 3 113 16 11 96 99 ...
$ punkte : num 93 76.5 79.5 85 66.5 71 56.5 77 59 63.5 ...
$ schlafdauer : num 6.2 5.3 5.5 7 6.5 6.4 5.7 6.8 5.4 6.8 ...
$ lernzeit : num 8.2 7 6.8 7.3 7.3 3.9 4.9 7.6 2.5 9.2 ...
$ nachhilfe : int 1 1 1 1 1 0 0 1 0 0 ...
$ zeugnis_mathe_roh : num 101.3 89.7 86.2 83.6 86.8 ...
$ zeugnis_mathe_punkte : int 13 11 10 10 10 11 9 10 9 10 ...
$ zeugnis_mathe_note : Factor w/ 4 levels "ausreichend",..: 1 2 2 2 2 2 3 2 3 2 ...
$ zeugnis_deutsch_punkte: int 8 9 10 6 10 10 9 12 5 13 ...
$ zeugnis_deutsch_note : Factor w/ 4 levels "ausreichend",..: 3 3 2 4 2 2 3 2 4 1 ...
$ lsport : Factor w/ 6 levels "Andere Sportart",..: 4 5 1 3 3 4 3 3 4 4 ...
$ sport_fb : int 0 1 0 1 1 1 1 1 1 1 ...
$ sport_bb : int 0 0 1 0 0 0 0 1 1 0 ...
$ sport_sw : int 1 1 1 1 0 0 1 1 1 1 ...
$ sport_tn : int 0 0 0 0 0 0 0 0 1 0 ...
$ sport_an : int 1 0 1 1 0 0 1 1 1 1 ...
$ sport_no : int 0 0 0 0 0 0 0 0 0 0 ...
$ sport_test : int 0 1 1 0 1 1 0 1 1 1 ...
$ kantine_zufr : int 4 4 3 5 3 2 2 1 3 2 ...
$ taschengeld : int 33 30 29 35 28 32 41 36 34 34 ...
$ lauf100 : num 14.3 13.2 13.9 14 15 14.2 14.1 14.8 15.2 13.8 ...
$ lauf1000 : num 234 229 210 222 227 ...
$ lauf5000 : num 489 465 484 486 461 ...
$ kugel : num 8.15 9.26 8.47 8.37 7.56 ...
$ lfach : Factor w/ 7 levels "anderes Fach",..: 2 2 2 2 2 2 2 2 2 2 ...Zu den einzelnen Variablen zeigt die Ausgabe deren Speicherformat (int für "integer", num für "numeric" - beides Zahlenwerte, Factor für nicht-numerische Variablen) und die jeweils ersten Werte im Datensatz.
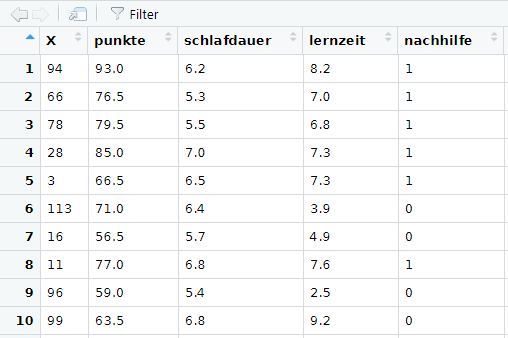
In der Benutzeroberfläche R-Studio liefert der Data Viewer zudem einen Einblick in den Datensatz als Datentabelle. Aufgerufen wird er mit der Funktion
View(dat)So sieht ein Ausschnitt aus dem Data Viewer aus:
Lagemaße anhand der Funktion summary()
Einen Überblick über die wichtigsten Lagemaße bietet die Funktion summary(). Die Funktion ist generisch, d.h. sie passt ihre Berechnungen der Art der Informationen (technisch: den Objekttypen) an, die sie erhält. Verwenden wir summary() z.B. auf die numerische Variable punkte, erhalten wir das arithmetische Mittel (Mean), den Median (Median) und das erste und das dritte Quartil (1st Qu. und 3rd Qu.) sowie den kleinsten und den größten Wert der Verteilung (Min. und Max.):
summary(dat$punkte)
Min. 1st Qu. Median Mean 3rd Qu. Max.
11.50 62.50 73.50 73.23 84.62 113.50 Für eine kategoriale Variable (vom Objekttyp Factor) erhalten wir mit der Funktion summary() anstelle einer Tabelle mit deskriptiven Statistiken die Häufigkeitstabelle der Verteilung. Für die Variable lsport:
summary(dat$lsport)
Andere Sportart Basketball Fußball
14 18 34
Keine Sportart Schwimmen Tennis
32 16 6Eine alternative Möglichkeit bietet das Paket "DescTools". Wir laden das Paket mit der Funktion library(DescTools). Falls das Paket nicht installiert ist, müssen wir dies einmalig nachholen:
install.packages("DescTools") # Installation nur einmalig notwendig
library(DescTools)Die Funktion Desc gibt die zentralen Statistiken direkt aus und stellt die Verteilung grafisch dar.
Desc(dat$punkte)
Desc(dat$lsport)Wenn wir an einzelnen Maßzahlen interessiert sind, können wir alle Lagemaße auch einzeln ermitteln:
Modalwert
Der Modalwertmuss wie oben gezeigt aus einer Häufigkeitstabelle abgelesen werden. Die von der summary()-Funktion für Factor-Variablen ausgegebene Tabelle erhalten wir auch mit table(). Auf die Variable lsport (Lieblingssport) angewendet
table(dat$lsport)erhalten wir das Ergebnis
Andere Sportart Basketball Fußball
14 18 34
Keine Sportart Schwimmen Tennis
32 16 6 Fußball kommt mit 34 Fällen am häufigsten vor. Die am häufigsten genannte Lieblingssportart ist Fußball.
Die Funktion typical_value() aus dem Paket "sjmisc" kann verwendet werden, um den Modus direkt zu berechnen. Das Paket muss dazu ggf. installiert und mit library() aktiviert werden. Als Option wird fun = "mode" angegeben, um den Modus zu erhalten. Hinweis: Die Funktion gibt auch für multimodale Verteilungen nur einen Modus aus. Im Zweifel muss in der Häufigkeitstabelle geprüft werden, ob mehrere Modi vorliegen.
install.packages("sjmisc") # Paket installieren
library(sjmisc) # Paket aktivieren
typical_value(dat$lsport, fun = "mode")
. [1] "Fußball"Median
Mit der Funktion median() lässt sich der Median eines Merkmals berechnen. Für das Merkmal lernzeit verwenden wir:
median(dat$lernzeit)und erhalten als Ergebnis einen Median von 6,9. Die Hälfte der Schüler*innen hat 6,9 oder weniger Stunden für den Test gelernt.
Quantile berechnen wir mit der Funktion quantile(). Mit der Option probs geben wir an, für welchen Anteil wir den Quantilwert berechnen wollen. Für das 1%-Quantil schreiben wir 0.01, für das 12%-Quantil 0.12, usw.
Wir möchten das 25%-Quantil (also das erste Quartil) sowie das 75%-Quantil (also das dritte Quartil) der Variable lernzeit bestimmen und nutzen die folgenden Befehle:
quantile(dat$lernzeit, probs=0.25)
quantile(dat$lernzeit, probs=0.75)Es können auch Quantile für mehrere Anteilwerte gleichzeitig berechnet werden:
quantile(dat$lernzeit, probs=c(0.25, 0.75))Das erste Quartil liegt bei 5,2 und das dritte Quartil liegt bei 8,1.
Ohne Angabe von Anteilswerten
quantile(dat$lernzeit)erhalten wir standardmäßig alle drei Quartile sowie das 0%- und das 100%-Quantil:
0% 25% 50% 75% 100%
0.700 5.225 6.900 8.100 12.200 2.200 Wir benutzen die Funktion mean() für die Berechnung des arithmetischen Mittels. Das arithmetische Mittel des der Variable punkte erhalten wir mit
mean(dat$punkte)
. [1] 73.23333Das arithmetische Mittel der Punktezahl beträgt 73,2. Durchschnittlich wurden in dem Test also 73 Punkte erreicht.
Wichtige Befehlsoptionen
na.rm = TRUE bei fehlenden Werten
Liegen bei einer Variable im Datensatz nicht für alle Beobachtungsfälle Daten vor, führen diese fehlenden Werte (in R als NA gekennzeichnet) bei der Berechnung von Median und arithmetischem Mittel zu dem Ergebnis
. [1] NA
Um die fehlenden Werte bei der Berechnung auszuschließen, muss explizit die Befehlsoption na.rm = TRUE angegeben werden:
mean(dat$punkte, na.rm = TRUE)
median(dat$punkte, na.rm = TRUE)Beispieldaten herunterladen: daten_stata.dta
Datenbeispiel
<!-- Das Datenbeispiel befindet sich in dem heruntergeladenden ZIP-Ordner. Dieser enthält neben dem Beispieldatensatz *daten_stata.dta* ein do-File, in dem die hier verwendeten Funktionen dokumentiert worden sind. -->Der Beispieldatensatz kann mit der Funktion use geladen werden. Dafür muss zusätzlich der korrekte Pfad zum Speicherort der Datei daten_stata.dta angegeben werden:
use "C:\...Pfad...\daten_stata.dta"
Einen Überblick über die wichtigsten Lagemaße bietet die Funktion summarize. Die Funktion gibt u.a. einen Überblick über die Anzahl der Beobachtungen (Obs), das arithmetische Mittel (Mean) sowie den kleinsten Wert (Min) und größten Wert (Max): <!---AN,13.05.2020: Ich denke die Standardabweichung (Std. Dev.) ist an dieser Stelle noch nicht von Bedeutung und sollte nicht zusätzliche Verwirrung schaffen.--->
summarize punkte
> Variable | Obs Mean Std. Dev. Min Max
-------------+---------------------------------------------------------
punkte | 120 73.23333 16.29455 11.5 113.5
Die summarize Funktion kann mit detail erweitert werden, sodass sie weitere Kennzahlen berechnet:
summarize punkte, detail
> punkte
-------------------------------------------------------------
Percentiles Smallest
1% 31 11.5
5% 48.5 31
10% 54 41 Obs 120
25% 62.5 44.5 Sum of Wgt. 120
50% 73.5 Mean 73.23333
Largest Std. Dev. 16.29455
75% 84.75 104.5
90% 93.75 106 Variance 265.5123
95% 101.5 106 Skewness -.3220941
99% 106 113.5 Kurtosis 3.974038
Neben den bereits bekannten Werten werden nun u.a. neun verschiedene Percentile (1%, 5%, 10%, 25%, 50%, 75%, 90%, 95%, 99%) und die vier kleinsten Ausprägungen (11.5 Punkte, 31 Punkte, 41 Punkte, 44.5 Punkte) sowie die vier größten Ausprägungen (104.5 Punkte, 106 Punkte, 106 Punkte, 113.5 Punkte) berechnet. Aus diesen Kennzahlen können der Median und die Quartile abgeleitet werden:
- der Median entspricht dem 50%-Percentil, also 73,5 Punkten
- das 0%-Quantil entspricht dem kleinsten Wert (11,5 Punkte), das erste Quartil ist gleich dem 25%-Quantil (62,5 Punkte), das zweite Quartil ist der Median (73,5 Punkte), das dritte Quartil ist das 75%-Quantil (84,75 Punkte) und das 100%-Quantil entspricht dem größten Wert (113,5 Punkte)
Die Funktion summarize eignet sich nicht für kategoriale Variablen wie z.B. lfach:
summarize lfach
> Variable | Obs Mean Std. Dev. Min Max
-------------+---------------------------------------------------------
lfach | 0
Für kategoriale Variablen ist tabulate besser geeignet, da die Funktion eine Übersicht über die Verteilung der Merkmalsausprägungen in Form einer Häufigkeitstabelle liefert:
tabulate lfach
> lfach | Freq. Percent Cum.
-------------+-----------------------------------
Deutsch | 24 20.00 20.00
Englisch | 21 17.50 37.50
Geschichte | 17 14.17 51.67
Mathematik | 17 14.17 65.83
Physik | 13 10.83 76.67
Sport | 13 10.83 87.50
anderes Fach | 15 12.50 100.00
-------------+-----------------------------------
Total | 120 100.00
Wenn wir nur an einzelnen Maßzahlen interessiert sind, können diese separat ermittelt werden.
Modalwert
Der Modalwert kann aus einer Häufigkeitstabelle abgelesen werden. Mit der Option sort der tabulate-Funktion erhalten wir eine Tabelle, in der
die Variablenausprägungen ihrer Häufigkeit nach geordnet dargestellt werden, so dass die Modal-Kategorie in der ersten Zeile steht. Für die Variable lsport ergibt sich "Fußball" als Modalwert:
tabulate lsport, sort
> lsport | Freq. Percent Cum.
----------------+-----------------------------------
Fußball | 34 28.33 28.33
Keine Sportart | 32 26.67 55.00
Basketball | 18 15.00 70.00
Schwimmen | 16 13.33 83.33
Andere Sportart | 14 11.67 95.00
Tennis | 6 5.00 100.00
----------------+-----------------------------------
Total | 120 100.00
Median, arithmetisches Mittel und Quartile
<!--AN, 19.06.2020 Es wäre ja auch möglich, die Kennzahlen über summarize und r() aufzurufen. Ich finde es aber sinnvoller diese Möglichkeit hier nicht zu zeigen. Wenn es nur um die Kennzahl geht, ohne damit nachher weitere Berechnungen anzustellen, ist tabstat die bessere Wahl.-->Mit der Funktion tabstat lassen sich einzelne Kennzahlen einer Variablen berechnen. Mit der stat() Option kann die gewünschte Maßzahl ausgewählt werden.
- Der Median wird mit der Option stat(median) berechnet:
tabstat lernzeit, stat(median)
> variable | p50
-------------+----------
lernzeit | 6.9
------------------------
Der Median für die Variable lernzeit beträgt 6,9. Die Hälfte der Schüler*innen hat 6,9 oder weniger Stunden für den Test gelernt.
-- Die Option stat(mean) gibt das arithmetischen Mittels aus:
tabstat punkte, stat(mean)
> variable | mean
-------------+----------
punkte | 73.23333
------------------------
Das arithmetische Mittel der Punktezahl beträgt ca. 73,2. Durchschnittlich wurden in dem Test also in etwa 73 Punkte erreicht.
Für die Berechnung des 25%- und 75%-Quantils kann stat(p25 p75) verwendet werden. Sollen ebenfalls das Minimum und das Maximum mit angegeben werden, wird die Funktion mit min und max erweitert:
tabstat lernzeit, stat(p25 p75)
> variable | p25 p75
-------------+--------------------
lernzeit | 5.15 8.1
----------------------------------
tabstat lernzeit, stat(min p25 p75 max)
> variable | min p25 p75 max
-------------+----------------------------------------
lernzeit | .7 5.15 8.1 12.2
------------------------------------------------------
Das erste Quartil liegt bei 5,2 Stunden und das dritte Quartil liegt bei 8,1 Stunden. Das Minimum ist 0,7 Stunden und das Maximum 12,2 Stunden.
Anmerkung: Die Kennzahlen werden immer in der Reihenfolge ausgegeben in der sie in dem Stata-Befehl notiert worden sind.
Beispieldaten herunterladen: dat.sav
Datenbeispiel
Arithmetisches Mittel, Median und Modalwert
Statt durch Klicken durch das Menü können wir uns die Lagemaße über die Syntax ausgeben lassen. Dazu verwenden wir den folgenden Code:
FREQUENCIES VARIABLES=punkte schlafdauer lsport
/STATISTICS=MEAN MEDIAN MODE.Wir verwenden den Befehl FREQUENCIES und geben nach VARIABLES= nacheinander alle gewünschten Variablen mit Leerzeichen getrennt an. Das Ergebnis wäre je eine Häufigkeitstabelle pro Variable. Um zusätzlich Lagemaße zu erhalten, geben wir den Unterbefehl /STATISTICS= ein mit den Optionen MEAN für das arithmetische Mittel, MEDIAN für den Median und MODE für den Modalwert. Mit dem Punkt schließen wir den Befehl ab.
Statt mit FREQUENCIES (im Menü: Analysieren -> Deskriptive Statistiken -> Häufigkeiten) können wir uns Maßzahlen alternativ mit DESCRIPTIVES berechnen. Dies kann bei metrischen Variablen mit großem Merkmalsraum von Vorteil sein, da keine Häufigkeitstabellen ausgegeben werden und über die Syntax schnell die gewünschten Maßzahlen angegeben werden können. Median und Modus können hierbei allerdings nicht ausgewählt werden. Wir verwenden entweder den Code
DESCRIPTIVES VARIABLES=punkte
/STATISTICS=MEAN.oder Klicken durch das Menü: Analysieren -> Deskriptive Statistiken -> Deskriptive Statistik -> Variablen auswählen -> Optionen -> Mittelwert -> weiter -> OK.
Weitere Artikel zu univariaten Verteilungen
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht-kommerziell - Weitergabe unter gleichen Bedingungen 4.0 International Lizenz.
Autor*innen dieses Artikels
Sebastian Gerhartz, Adrian Neuser, Lisa Rüge
Diese Seite wurde zuletzt am 15.01.2024 aktualisiert.